Notice
We only slove the third problem in div.2 and the first two problems of div.1.
If the author want, we also provide solution to the third problem in div.1.
Meaning
SRM 616 div.2
T3: TwoLLogo
- —> goto Hint
- —> goto Tutorial
- Time Limist : 3000 MS
- Memory Limist : 256 MB
- Author : yanyikai
你有一个$n×m$的矩阵, 由
.于#组成, 你可以在.上放两个$L$型(不可旋转), $L$型两端的长度$>2$, 求方案数.
SRM 616 div.1
T1: WakingUp
- —> goto Hint
- —> goto Tutorial
- Time Limist : 2000 MS
- Memory Limist : 256 MB
- Author : yanyikai
你有一个初值, 每分钟会加上, 你有个操作, 每个操作表现为, 在第分钟使减去.
你要求最大的初值, 使有可能, 如果趋向无穷大, 输出-1.
T2: ColorfulCoins
- —> goto Hint
- —> goto Tutorial
- Time Limist : 2000 MS
- Memory Limist : 256 MB
- Author : yanyikai
有种硬币面值是, 满足各不相同, 且, 你每次可以询问一个, 然后得到由最少硬币组成的, 硬币大小相同, 不同面值颜色不同, 问最少多少次询问可以得出所有面值的硬币的颜色.
SRM 617 div.2
T3: MyVeryLongCake
- —> goto Hint
- —> goto Tutorial
- Time Limist : 2000 MS
- Memory Limist : 256 MB
- Author : yanyikai
你有长度为的木板, 你要将其分成若干段, 使对于所有, 你都能拼出个长度相同的木板, 最小化段数.
SRM 617 div.1
T1: MyLongCake
- —> goto Hint
- —> goto Tutorial
- Time Limist : 2000 MS
- Memory Limist : 256 MB
- Author : yanyikai
你有长度为的木板, 你要将其分成若干段, 使对于所有, 你都能拼出个长度相同的木板, 最小化段数
(同上, 双倍经验).
Hint
SRM 616 div.2
T3: TwoLLogo
- —> return Meaning
- —> goto Tutorial
Hint 1:
我们考虑$n^8$暴枚两个$L$型, 期望$T$飞.
Hint 2:
考虑枚举两个$L$型的转折点.
此时有四种情况(红色的边为限制边):
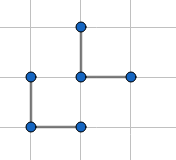
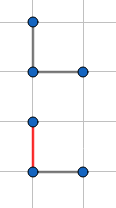
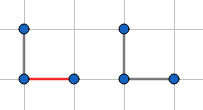
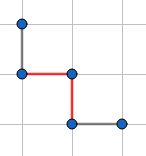
然后$n^4$$AC$-> Tutorial.
Hint 3(踩标算):
考虑所有方案减去不合法的方案数, 仅有三种不合法状态(红点为转折点):
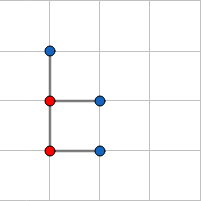
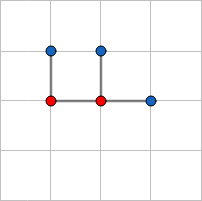
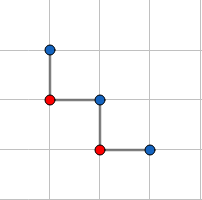
然后$n^2$秒$A$-> Tutorial.
SRM 616 div.1
T1: WakingUp
- —> return Meaning
- —> goto Tutorial
Hint 1:
仔细观察数据范围, 发现的
LCM, 且每分钟减去的值会有循环.
T2: ColorfulCoins
- —> return Meaning
- —> goto Tutorial
Hint 1:
样例3: 询问5, 6, 此时只有4出现两次, 于是可以推出三种硬币的颜色.
如果询问7, 1, 2, 3各一个, 无法分辨出每一个硬币单独的颜色.
Hint 2:
设, 询问次可以分辨出的硬币种数为.
(垃圾结论, 毁我青春)
SRM 617 div.2
T3: MyVeryLongCake
- —> return Meaning
- —> goto Tutorial
Hint 1:
直接在中找的点, 去重就好了.
Hint 2:
优化时间复杂度, 的范围是.
SRM 617 div.1
T1: MyLongCake
- —> return Meaning
- —> goto Tutorial
Hint 1:
直接在中找的点, 去重就好了
(时间复杂度什么的就算了…).
Tutorial
SRM 616 div.2
T3: TwoLLogo
- —> return Meaning
- —> return Hint
$n^4$标算(Hint-2):
我们考虑预处理以当前点为中转点, 向上和向右最长延伸长度$(up[][],right[][])$.
设第一个$L$型为($x_0$,$y_0$), 第二个$L$型为($x_1$,$y_1$).
- $answer$直接加上即可.
- 由于有可能被($x_1$,$y_1$)挡住, 所以要与取$min$.
- 同理
2.- 随便分类搞一下, 注意重叠的方案.
Code:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int up[N][N],ri[N][N],mp[N][N];
long long TwoLLogo::countWays(vector <string> grid) {
int n=grid.size(),m=grid.begin()->size();
M(up);M(ri);long long ans=0;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
mp[i+1][j+1]=grid[i][j]=='.';
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
{
if(!mp[i][j])continue;
for(int k=i-1;k&&mp[k][j];--k)
++up[i][j];
for(int k=j+1;k<=m&&mp[i][k];++k)
++ri[i][j];qujin
}
for(int x0=1;x0<=n;++x0)
for(int y0=1;y0<=m;++y0)
if(mp[x0][y0])
{
//处理2, 使剩下来的y1>y0.
for(int x1=x0+1;x1<=n;++x1)
if(mp[x1][y0])
ans+=1ll*up[x0][y0]*ri[x0][y0]*min(up[x1][y0],x1-x0-1)*ri[x1][y0];
for(int x1=1;x1<=n;++x1)
for(int y1=y0+1;y1<=m;++y1)
if(mp[x1][y1])
{
//3.
if(x0==x1)ans+=1ll*up[x0][y0]*min(ri[x0][y0],y1-y0-1)*up[x1][y1]*ri[x1][y1];else
//1.
if(x0>x1)ans+=1ll*up[x0][y0]*ri[x0][y0]*up[x1][y1]*ri[x1][y1];else
//4.
ans+=1ll*up[x0][y0]*ri[x1][y1]*min(y1-y0-1,ri[x0][y0])*max(up[x1][y1]-x1+x0+1,0),
ans+=1ll*up[x0][y0]*ri[x1][y1]*ri[x0][y0]*min(x1-x0-1,up[x1][y1]);
}
}
return ans;
}
$n^2$踩标算(Hint-3):
处理出$left[][]$为$up[][]$的两个
#之间的横向前缀和, $down[][]$为$right[][]$的两个#之间的纵向前缀和.
- 枚举列和两个点, , 且 之间没有
#.
贡献为:
<==>- 枚举行和两个点, , 且 之间没有
#.
贡献为:
<==>- 枚举交点$(x,y)$, 另外两个转折点为, ,
且 之间没有#贡献为: <==>注意: 答案初值可能会暴
longlong, 可以%一个大质数来维护答案…
Ps: 不保证代码正确性(没有取%很难写)…
Code:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int up[N][N],ri[N][N],le[N][N],dw[N][N],mp[N][N];
long long TwoLLogo::countWays(vector <string> grid) {
int n=grid.size(),m=grid.begin()->size();
M(up);M(ri);M(le);M(dw);unsigned long long ans=0,res=0,sum=0;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)
mp[i][j]=grid[i][j]=='.';
for(int i=1;i<=n;++i)
for(int j=m;j;--j)
if(mp[i][j])
{
up[i][j]=(i-1)&&mp[i-1][j]?up[i-1][j]+1:0;
ri[i][j]=(j-m)&&mp[i][j+1]?ri[i][j+1]+1:0;
}
for(int i=n;i;--i)
for(int j=1;j<=m;++j)
if(mp[i][j])
{
le[i][j]=(j-1)?le[i][j-1]+up[i][j-1]:0;
dw[i][j]=(i-n)?dw[i+1][j]+ri[i+1][j]:0;
}
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if(mp[i][j])
res+=1ll*ri[i][j]*up[i][j]*dw[i][j]*(up[i][j]+1),
res+=1ll*ri[i][j]*up[i][j]*le[i][j]*(ri[i][j]+1),
res+=1ll*le[i][j]*ri[i][j]*dw[i][j]*up[i][j],
ans+=1ll*sum*up[i][j]*ri[i][j],sum+=up[i][j]*ri[i][j];
return ans-res;
}
SRM 616 div.1
T1: WakingUp
- —> return Meaning
- —> return Hint
暴力处理1~2e6分钟的, 易知当时, 第分钟减去的值等于第分钟减去的值.
对1~2e6分钟的取$min$, 如果的值在第分钟后还有更新, 那么趋近无穷大.
Code:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int del[N];
int WakingUp::maxSleepiness(vector <int> period, vector <int> start, vector <int> volume, int D) {
int n=start.size(),ans=0,now=0,lcm=1;M(del);
for(int i=0;i<n;++i)
for(int j=start[i];j<N;j+=period[i])
del[j]+=volume[i];
for(int i=0;i<n;++i)
lcm*=period[i]/__gcd(period[i],lcm);
for(int i=1;i<N;++i){
now+=D-del[i];
if(now<ans&&i>5*lcm+100)
return -1;
if(now<ans)ans=now;
}
return -ans;
}
T2: ColorfulCoins
- —> return Meaning
- —> return Hint
先对排序, 然后求个前缀和,
Code:
都这样了你还想要代码???
SRM 617 div.2
T3: MyVeryLongCake
- —> return Meaning
- —> return Hint
题意转化为求的个数, 同理于, 及为.
, 记, 则.
然后筛个质因子就好了, 其实还可以容斥来筛, 这里就不打了.
Code:1
2
3
4
5
6
7
8
9
10int a[15],tot;
int MyVeryLongCake::cut(int n) {
int _n=n,__n=n;tot=0;
for(int i=2;i*i<=n;++i)
if(n%i==0)
for(a[++tot]=i;n%i==0;n/=i);
if(n!=1)a[++tot]=n;
for(int i=1;i<=tot;++i)_n-=n/a[i];
return __n-_n;
}
SRM 617 div.1
T1: MyLongCake
- —> return Meaning
- —> return Hint
题意转化为求的个数, 同理于, 及为.
欧拉函数直接筛就好了, 反正双倍经验 + 数据范围变小.
Code:1
2
3
4
5
6
7
8
9
10int a[15],tot;
int MyVeryLongCake::cut(int n) {
int _n=n,__n=n;tot=0;
for(int i=2;i*i<=n;++i)
if(n%i==0)
for(a[++tot]=i;n%i==0;n/=i);
if(n!=1)a[++tot]=n;
for(int i=1;i<=tot;++i)_n-=n/a[i];
return __n-_n;
}